HOJA DE CALCULO

HOJAS DE CALCULO

 

Orígenes de las hojas de cálculo

En 1961 se vislumbró el concepto de una hoja de cálculo electrónica en el artículo Budgeting Models and System Simulation de Richard Mattessich. Pardo y Landau merecen parte del crédito de este tipo de programas, y de hecho intentaron patentar (patente en EE.UU. número 4.398.249) algunos de los algoritmos en 1970. La patente no fue concedida por la oficina de patentes por ser una invención puramente matemática. Pardo y Landau ganaron un caso en la corte estableciendo que "algo no deja de ser patentable solamente porque el punto de la novedad es un algoritmo". Este caso ayudó al comienzo de las patentes de software.

Dan Bricklin es el inventor generalmente aceptado de las hojas de cálculo. Bricklin contó la historia de un profesor de la universidad que hizo una tabla de cálculos en una pizarra. Cuando el profesor encontró un error, tuvo que borrar y reescribir una gran cantidad de pasos de forma muy tediosa, impulsando a Bricklin a pensar que podría replicar el proceso en un computador, usando el paradigma tablero/hoja de cálculo para ver los resultados de las fórmulas que intervenían en el proceso.

Su idea se convirtió en VisiCalc, la primera hoja de cálculo, y la "aplicación fundamental" que hizo que el PC (ordenador u computador personal) dejase de ser sólo un hobby para entusiastas del computador para convertirse también en una herramienta en los negocios y en las empresas.

Varias informaciones acerca de los sistemas de información y algunas personas, confirman que la primera hoja electrónica, llamada Visicalc fue creada en el año 1978 por Daniel Bricklin, quien fue alumno de la facultad de negocios de Harvard, además cabe mencionar que fue él quien inventó las Hojas Electrónicas. Bricklin supuestamente estaba preparando una Hoja Electrónica para un HBS (caso de estudio) y para la creación de esta tenía dos alternativas 1.-Hacerlo a mano, o 2.-Usar una terminal de tiempo compartido que usaba un Mainframe. Bricklin, quería hacer un programa donde los usuarios obtuvieran la capacidad de visualizar una hoja cuadriculada tal y como los Contadores hacían a mano. Su visión era “una pizarra electrónica y una tiza electrónica.

Para el verano de 1978, Bricklin ya había programado su primera versión ejecutable de su concepto. El programa le permitía al usuario insertar matrices de 5 columnas y 20 filas. La primera versión no era fácil de manejar y, debido a ésto Bricklin contrató a Bob Frankston, para así poder expandir la facilidad de uso del programa. Frankston expandió el programa a tal punto que redujo los requerimientos de éste, haciéndolo más poderoso y práctico para poder ser utilizado en un Microcomputador.Durante el verano de 1978, Daniel Flystra se unió a Bricklin y a Frankston. Flystra era mercadologo y sugirió que el producto podría ser de gran demanda si pudiera correrse en un computador Apple Macintosh. Entre los tres formaron una compañía conocida por el nombre de Software Arts Corporation la cual fue fundada en enero de 1979 y era dirigida por Bricklin. En Abril de ese mismo año, la compañía comenzó a distribuir a Visicalc, cuyo nombre fue tomado de una abreviatura hecha de las palabras en inglés “Visible Calculator” (Calculadora Visible).Visicalc se convirtió en un fenómeno en la época de los 80 e incentivó a muchos negociantes a comprar Computadores Personales (PC). Más de 1 millón de copias fueron vendidas durante la producción total de Visicalc.

Celdas

Una celda de una hoja de cálculo es el lugar donde se pueden introducir datos o realizar cálculos, visualmente es un espacio rectangular que se forma en la intersección de una fila y una columna y se les identifica con un nombre, como por ejemplo C4 (C es el nombre de la columna y 4 el de la fila).

Las filas son horizontales y están identificadas por los números en secuencia ascendente. Las columnas en cambio están identificadas con las letras del alfabeto y van de forma vertical en la Hoja de Cálculo.

En las celdas se introduce cualquier tipo de información como texto o números, y también fórmulas o instrucciones para realizar un determinado cálculo o tarea.

En 1961 se vislumbró el concepto de una hoja de cálculo electrónica en el artículo Budgeting Models and System Simulation de Richard Mattessich. Pardo y Landau merecen parte del crédito de este tipo de programas, y de hecho intentaron patentar (patente en EE.UU. número 4.398.249) algunos de los algoritmos en 1970. La patente no fue concedida por la oficina de patentes por ser una invención puramente matemática. Pardo y Landau ganaron un caso en la corte estableciendo que "algo no deja de ser patentable solamente porque el punto de la novedad es un algoritmo". Este caso ayudó al comienzo de las patentes de software.

Dan Bricklin es el inventor generalmente aceptado de las hojas de cálculo. Bricklin contó la historia de un profesor de la universidad que hizo una tabla de cálculos en una pizarra. Cuando el profesor encontró un error, tuvo que borrar y reescribir una gran cantidad de pasos de forma muy tediosa, impulsando a Bricklin a pensar que podría replicar el proceso en un computador, usando el paradigma tablero/hoja de cálculo para ver los resultados de las fórmulas que intervenían en el proceso.

Su idea se convirtió en VisiCalc, la primera hoja de cálculo, y la "aplicación fundamental" que hizo que el PC (ordenador u computador personal) dejase de ser sólo un hobby para entusiastas del computador para convertirse también en una herramienta en los negocios y en las empresas.

Varias informaciones acerca de los sistemas de información y algunas personas, confirman que la primera hoja electrónica, llamada Visicalc fue creada en el año 1978 por Daniel Bricklin, quien fue alumno de la facultad de negocios de Harvard, además cabe mencionar que fue él quien inventó las Hojas Electrónicas. Bricklin supuestamente estaba preparando una Hoja Electrónica para un HBS (caso de estudio) y para la creación de esta tenía dos alternativas 1.-Hacerlo a mano, o 2.-Usar una terminal de tiempo compartido que usaba un Mainframe. Bricklin, quería hacer un programa donde los usuarios obtuvieran la capacidad de visualizar una hoja cuadriculada tal y como los Contadores hacían a mano. Su visión era “una pizarra electrónica y una tiza electrónica.

Para el verano de 1978, Bricklin ya había programado su primera versión ejecutable de su concepto. El programa le permitía al usuario insertar matrices de 5 columnas y 20 filas. La primera versión no era fácil de manejar y, debido a ésto Bricklin contrató a Bob Frankston, para así poder expandir la facilidad de uso del programa. Frankston expandió el programa a tal punto que redujo los requerimientos de éste, haciéndolo más poderoso y práctico para poder ser utilizado en un Microcomputador.Durante el verano de 1978, Daniel Flystra se unió a Bricklin y a Frankston. Flystra era mercadologo y sugirió que el producto podría ser de gran demanda si pudiera correrse en un computador Apple Macintosh. Entre los tres formaron una compañía conocida por el nombre de Software Arts Corporation la cual fue fundada en enero de 1979 y era dirigida por Bricklin. En Abril de ese mismo año, la compañía comenzó a distribuir a Visicalc, cuyo nombre fue tomado de una abreviatura hecha de las palabras en inglés “Visible Calculator” (Calculadora Visible).Visicalc se convirtió en un fenómeno en la época de los 80 e incentivó a muchos negociantes a comprar Computadores Personales (PC). Más de 1 millón de copias fueron vendidas durante la producción total de Visicalc.

Celdas

Una celda de una hoja de cálculo es el lugar donde se pueden introducir datos o realizar cálculos, visualmente es un espacio rectangular que se forma en la intersección de una fila y una columna y se les identifica con un nombre, como por ejemplo C4 (C es el nombre de la columna y 4 el de la fila).

Las filas son horizontales y están identificadas por los números en secuencia ascendente. Las columnas en cambio están identificadas con las letras del alfabeto y van de forma vertical en la Hoja de Cálculo.

En las celdas se introduce cualquier tipo de información como texto o números, y también fórmulas o instrucciones para realizar un determinado cálculo o tarea.

Operaciones aritméticas básicas en plantillas de cálculo

 

Cada vez que se insertan datos en una celda, es posible observar que, por ejemplo, los datos literales o de texto se alinean a la izquierda de la celda mientras que un dato tipo numérico (entero o con decimales) se alinea a la derecha de la celda de forma automática.

Sin embargo, puede decirse que cada vez que se necesita hacer uno o más cálculos en una celda, es necesario escribir el cálculo de un modo diferente.

Existen operadores aritméticos básicos como la suma, la diferencia, el producto y el cociente que permiten realizar dichos cálculos, existen además funciones predeterminadas para dicho fin. En todos los casos, debe anteponerse el signo igual (=) a todos estos tipos de cálculos para que la plantilla “reconozca” a ese dato como una operación aritmética o función sobre determinado dato o grupo de datos.

Las cuatro operaciones básicas en plantillas: Suma, resta, producto y cociente

La multiplicación se realiza por medio del operador *. Por ejemplo =b1*c3, multiplica los valores que hay en las celdas b1 y c3. Se pueden multiplicar más de dos celdas.

La división se realiza por medio del operador /. Por ejemplo =b1/c3, divide el valor que hay en la celda b1 por el de la celda c3.

Si se desea elevar el valor de una celda al exponente n, debe utilizarse el símbolo circunflejo (^). Por ejemplo, para elevar el contenido de la celda c4 al cubo se escribe la fórmula =c4^3.

Si la suma es de pocas celdas, conviene sumarlas directamente: =a1+a2+a3. Lo mismo puede hacerse si necesita restarse: =a1-b1-c1.

Símbolos de agrupación de operaciones

Cuando se deben hacer operaciones combinadas (divisiones que se suman a una multiplicación, por ejemplo), se pueden usar paréntesis como en matemática para separar una operación de otra. Sin embargo, y también del mismo modo que en matemática, las operaciones tienen un Orden de Prioridad “natural” de operación. Primero se resuelven potencias y raíces. Después cocientes y productos.

Orden de prioridad de las operaciones

Todas las subexpresiones entre paréntesis se evalúan primero. Las subexpresiones con paréntesis anidados se evalúan desde el centro hacia los extremos.

Dentro de una expresión, los operadores se evalúan de la siguiente manera:

° Se analiza la expresión de izquierda a derecha.

° Si en la expresión existen paréntesis, lo que se encuentra dentro de estos se evalúan de izquierda a derecha según orden de prioridad de los mismos.

° Si en la expresión se encuentran más de un par de paréntesis, la evaluación se realiza comenzando con el paréntesis que se encuentra más a la izquierda en la expresión hasta llegar al par de paréntesis que se encuentra más a la derecha de la expresión.

Nociones de constantes y variables

Un par de conceptos de vital interés en matemática, y en toda aplicación de esta ciencia a un área específica de conocimiento, es el de constante y variable. Para emplear una terminología simple, entenderemos por constante todo número (o más genéricamente todo valor) conciso.

Una variable en cambio, y como su nombre lo sugiere, es una representación de un dato que puede no tener el mismo valor siempre.

Así, cuando decimos La temperatura de ebullición del agua es de 100º C, estamos haciendo referencia a un valor constante para ese fenómeno en particular. Sin embargo si hacemos referencia a la experiencia de calentar el agua, observaremos que a medida que transcurre el tiempo, los valores que toma la temperatura van variando hasta alcanzar la ebullición. En este segundo caso, a la temperatura se la considera variable.

Operaciones con constantes

La plantilla de cálculo Excel, por supuesto, puede manipular de forma directa valores específicos (constantes), de modo similar a una calculadora.

Así, si se desean sumar los números 12, 13, 12 y 14 que están en las celdas a1, a2, a3 y a4 respectivamente, será suficiente con posicionarse, por ejemplo, en la celda a5 y escribir =12+13+12+14.

Como se verá a continuación, esta forma de realizar cálculos (complejos o no), no es recomendable. Cometer un error en la carga de un valor implicaría corregir el número erróneo, y además la fórmula en sí misma.

Operaciones con variables. Ventajas

Puede añadirse a todo lo anteriormente expuesto que en Ciencias de la Computación, la interpretación de constante y de variable es similar a la de matemática, pero tiene además un enfoque particular en lo referente a la idea de variable.

Se considera que toda variable, en informática, almacena un valor. De este modo será mucho más ventajoso manipular una variable, y no su contenido específico. En la Planilla de Cálculo Excel, manipular variables equivale a manipular celdas.

De este modo, en el ejemplo anterior, será más eficiente escribir en la celda a5 la fórmula “con variables” =a1+a2+a3+a4, que la fórmula “con constantes” =12+13+12+14. En la primera, si se comete un error al cargar los valores de a1 a a4, solamente se corregirá/n dicho/s error/es. Como la fórmula está escrita “en celdas” – o sea manipulando variables – la fórmula en sí misma recalculará el resultado correcto sin necesidad de ser corregida.

Una fórmula es una secuencia formada por valores constantes, referencias a otras celdas, nombres, funciones, u operadores. Una fórmula es una técnica básica para el análisis de datos. Se pueden realizar diversas operaciones con los datos de las hojas de cálculo como *, +, -, Seno, Coseno, etc... En una fórmula se pueden mezclar constantes, nombres, referencias a otras celdas, operadores y funciones. La fórmula se escribe en la barra de fórmulas y debe empezar siempre por el signo =.

Los distintos tipos de operadores que se pueden utilizar en una fórmula son : Operadores aritméticos se emplean para producir resultados numéricos. Ejemplo: + - * /  % ^ Operador tipo texto se emplea para concatenar celdas que contengan texto. Ejemplo: & Operadores relacionales se emplean para comparar valores y proporcionar un valor lógico (verdadero o falso) como resultado de la comparación. Ejemplo: < > = <= >= <> Operadores de referencia indican que el valor producido en la celda referenciada debe ser utilizado en la fórmula. En Excel pueden ser: - Operador de rango indicado por dos puntos (:), se emplea para indicar un rango de celdas. Ejemplo: A1:G5 - Operador de unión indicado por una coma (,), une los valores de dos o más celdas. Ejemplo: A1,G5

Cuando hay varias operaciones en una misma expresión, cada parte de la misma se evalúa y se resuelve en un orden determinado. Ese orden se conoce como prioridad de los operadores. Se pueden utilizar paréntesis para modificar el orden de prioridad y forzar la resolución de algunas partes de una expresión antes que otras.

Las operaciones entre paréntesis son siempre ejecutadas antes que las que están fuera del paréntesis. Sin embargo, dentro de los paréntesis se mantiene la prioridad normal de los operadores. Cuando hay expresiones que contienen operadores de más de una categoría, se resuelve antes las que tienen operadores aritméticos, a continuación las que tienen operadores de comparación y por último las de operadores lógicos .

Los operadores de comparación tienen todos la misma prioridad, es decir que son resueltos de izquierda a derecha, en el orden en que aparecen. Son: Comparación Igualdad (=) Desigualdad (<>) Menor que (<) Mayor que (>) Menor o igual que (<=) Mayor o igual que (>=)

Los operadores lógicos y aritméticos son resueltos en el siguiente orden de prioridad (de mayor a menor): Aritméticos Lógicos Exponenciación (^) Not Negación (-) And Multiplicación (*) y División (/) Or Adición (+) y Sustracción (-) Concatenación de caracteres (&) Cuando hay multiplicación y división en la misma expresión, cada operación es resuelta a medida que aparece, de izquierda a derecha. Del mismo modo, cuando se presentan adiciones y sustracciones en una misma expresión, cada operación es resuelta en el orden en que aparece, de izquierda a derecha. El operador de concatenación de cadenas de caracteres (&) no es realmente un operador aritmético pero es prioritario respecto a todos los operadores de comparación.

Funciones Una función es una fórmula especial escrita con anticipación y que acepta un valor o valores, realiza unos cálculos con esos valores y devuelve un resultado. Todas las funciones tienen que seguir una sintaxis y si ésta no se respeta Excel nos mostrará un mensaje de error. 1) Los argumentos o valores de entrada van siempre entre paréntesis. No dejes espacios antes o después de cada paréntesis. 2) Los argumentos pueden ser valores constantes (número o texto), fórmulas o funciones. 3) Los argumentos deben de separarse por un punto y coma ";". Ejemplo: =SUMA(A1:B3) esta función equivale a =A1+A2+A3+B1+B2+B3

Referencias relativas

Cuando escribimos una fórmula, cualquiera que sea, podemos evitar escribirla muchas veces por medio del punto de autorellenado, que está en la celda seleccionada abajo a la derecha. Si nos ubicamos en la celda que contiene la fórmula, y acercamos el ratón a ese punto hasta que el puntero se transforma en una cruz finita y negra, puede apretarse el botón sin soltarse y "arrastrar" la fórmula al resto de las celdas. Cuando esto se hace de arriba para abajo, el número de la fila de la celda inicial se va incrementando en uno, y la letra de la columna queda fija. O sea que si la primera celda (la que contenía la fórmula), era c2, el autollenado celda por celda va siendo c3, c4, c5,…, c7, (suponiendo que la última sea c7). Si lo mismo se hace, por ejemplo, de izquierda a derecha, ocurre al revés. El número de la fila queda fijo, pero aumenta en uno la letra de la columna. O sea que si la primera celda (la que contenía la fórmula), era c2, el autollenado celda por celda va siendo d2, e2, f2,…, j2, (suponiendo que la última sea j2).

Referencias absolutas

Muchas veces ocurre que un valor en una celda debe afectar a varios valores que se encuentran en otro grupo de celdas. Por ejemplo, en una celda puede haber un precio que debe multiplicar a varias cantidades que se encuentran en otras celdas; o un porcentaje (de descuento o de incremento) debe multiplicar a varios importes que están en otro rango de celdas. Para poder utilizar la celda de precios, por ejemplo, para realizar las multiplicaciones, no podríamos autollenar la fórmula de multiplicación para todas las celdas. ¿Por qué?, porque como el número de la fila aumenta (es relativa), ya la celda del precio no multiplicaría a todos los números. Entonces, cuando se tiene que multiplicar un número en una celda por varios números que están en otras celdas, lo que conviene es inmovilizar la celda que contiene el precio. Esto se llama hacer una celda o referencia absoluta. Hay dos maneras de hacer esto. La primera es colocar el cursor (con el mouse o las teclas de dirección) delante de la celda que se quiere inmovilizar y pulsar la tecla F4. Supongamos que nuestro precio se encuentra en la celda b1 y la deseamos multiplicar por una primera cantidad de artículos que está en la celda c5. Cuando escribamos esa primera fórmula quedará =b1*c5. Para inmovilizar la celda b1 que tiene el precio por artículo, colocamos el cursor delante de la celda b1 (es decir entre el signo "=" y la "b" de b1) y después de pulsar la tecla F4, la fórmula quedará: =$b$1*c5, con lo cual ya la celda b1 está inmovilizada y al autollenar, no se modificará ni la letra "b" de la columna, ni el número 1 de la fila. Hecho esto, todos los números c5, c6, c7,…. Quedarán multiplicados por lo que hay en b1.

La otra manera de hacerlo es directamente tipear el signo $ delante de la b y el mismo signo delante del número 1 al escribir la fórmula. Del mismo modo anterior, la fórmula se podrá autollenar al resto de las celdas.

Ordenamiento de datos

Si lo que se desea es ordenar un conjunto de datos, debe seleccionarse el mismo (inclusive los rótulos) y puede ordenarse directamente en base a la primera columna (columna A), utilizando los botones A-Z (ascendente) o Z-A (descendente). Si se quiere ordenar por alguna otra columna que no sea la primera (la A), hay que seleccionar todos los datos (con rótulos y todo) e ir a DATOS y elegir la opción Ordenar… En el cuadro que aparece, arriba de todo permite elegir de una lista desplegable por cuál rótulo de columna quere ser la primera también), y a la derecha aparece si queremos que el ordenamiento sea ascendente o descendente.

Hojas de cálculo en el mercado

 

• Calc,OpenOffice.org
• Calc, integrada en LibreOffice
• Gnumeric, integrada en Gnome Office
• Hoja de cálculo, integrada en Google Apps.
• KSpread, integrada en KOffice, paquete gratuito de Linux.
• Lotus 1-2-3 integrada en Lotus SmartSuite
• Microsoft Excel, integrada en Microsoft Office
• Numbers, integrada en iWork de Apple
• StarOffice Calc, integrada en StarOffice.
• PlayMaker, integrada en SoftMaker Office.
• Corel Quattro Pro, integrada en WordPerfect.

PLANTILLAS DE CALCULO

INTRODUCCIÓN

El uso de una computadora ha llegado a evolucionar el trabajo, tal es el caso de trabajar en hojas de cálculo para agilizar tareas contables, financieras, matemáticas...

Se le asigna el nombre de hoja de cálculo a un hoja que esta divida en renglones y columnas, al cruce de ellos se le denomina celdas sobre las cuales se almacena información (letras o números) que podemos usar para realizar operaciones, tales como sumas, restas, multiplicaciones, divisiones, cálculos financieros, estadisticos, de ingeniería, amortizaciones, etc.

Por su parte, las hojas de cálculo no son simples celdas para introducir números con los que realizar diferentes operaciones: son herramientas que permiten tratar esos números y hacer gráficos o exportarlos a otros documentos.

I. PLANILLAS DE CALCULO

Las planillas de cálculos electrónicas o computarizadas son de origen mucho reciente. Muchas revistas le otorgan a Dan Bricklin el título de "padre" de las planillas de cálculo electrónicas.

1.1 Definición

Una planilla de cálculo es un programa que permite a los usuarios realizar tareas sin hacer ningún tipo de programación.

Cada celda de esta planilla, puede contener 3 tipos de entradas:

• Información numérica, por ejemplo números;
• Información alfabética o alfanumérica (palabras, letras, caracteres, números no utilizados en un cálculo) y
• Columnas con fórmulas, usualmente comenzadas con letras de celdas.

1.2 Usos

Usos generales de las planillas de cálculo:

• Almacenamiento de datos;
• Cálculos completos, por ejemplo presupuestos;
• Aplicaciones en matemática (teoremas, graficando funciones polinominales, aproximación de raíces irracionales, hipótesis); comparaciones, estadísticas, encuestas… 

II. LOTUS 1-2-3

2.1 Definición

Lotus es el primer programa de hoja de cálculo en introducir rangos de celdas, macros para las planillas y celdas con nombres. Con Lotus 1-2-3 es más fácil la utilización de planillas de cálculo y agrega la posibilidad de hacer gráficos y bases de datos.

Lotus 1-2-3 es aún uno de los paquetes de aplicaciones más vendido de todos los tiempos.

2.2 Beneficios y Productividad

• Lotus 1-2-3 estableció el software de planillas de cálculo como un paquete de presentación de datos importantes así como una herramienta de cálculo compleja.
• Ofrece a los usuarios herramientas que les permiten alcanzar el trabajo realizado rápidamente y con mayor eficiencia.
• AutoTotal permite sumar una serie de números con sólo tipear la palabra "Total", automáticamente se abre la más amplia función de planilla de cálculo.
• Lotus InfoBox es una herramienta de tarea sensitiva que ofrece a los usuarios información sobre cualquier selección de objeto y les permite fácil y rápidamente cambiar la selección de propiedades. Toda la edición es dinámica para brindar a los usuarios una respuesta intantánea de sus elecciones.
• Impresión dinámica previa permite a los usuarios editar simultáneamente y pre-ver sus hojas de trabajo. Con esta función los usuarios pueden ver instantáneamente el efecto de los cambios que realizaron en el rango de impresión de su hoja de trabajo antes de imprimir.
• Outlining ofrece la opción de realizar rápidamente un sumario de los datos de la hoja de trabajo dentro del formato outline. Los usuarios pueden focalizarse en los detalles para proveer un sumario visual top-line de su trabajo, que pueden imprimir con cualquier hoja de trabajo 1-2-3.
• Lotus Chart simplifica la creación de los más complejos cuadros. Debido a que éste es un componente compartido en SmartSuite, los usuarios pueden aprovechar esta capacidad con integración entre 1-2-3 y otras aplicaciones SmartSuite. La aplicación Lotus Chart ofrece la posibilidad a los usuarios de facilitar la creación de cuadros adaptados, un nuevo rango de nuevos cuadros 3D, múltiples tipos y tabulados y mejorar la edición, formato y manipulación de todos los elementos del cuadro.
• Títulos de hojas de trabajo pueden ahora ser seteadas a través de un paso rápido. Los usuarios pueden modificar el tamaño o el contenido de los títulos de la hoja simplemente clickeando y trasladando dentro del cuadro de la hoja de trabajo hacia una columna donde el titulo finaliza.
• Aplicaciones SmartSuite 1-2-3 son diseñadas para trabajar juntas y hacerles más fácil a los usuarios completar las tareas de aplicación comunes. Todas las aplicaciones SmartSuite de 32 bits comparten los mismos elementos de la interface de usuario, así como también herramientas comunes tales como Lotus Chart, y SmartCenter.
• 1-2-3 y Lotus Approach ahora pueden trabajar mejor en conjunto para ofrecer a los usuarios todo el poder de la base de datos de Approach en 1-2-3. Los usuarios pueden acceder a la poderosa funcionalidad de Approach para conducir datos, crear formatos, niveles de mail y reportes directamente desde 1-2-3.
• Una característica importante de Lotus 1-2-3 es que es compatible casi al 100 % con el sistema operativo UNIX.

III. EXCELL

3.1 Definición

Excel fue originalmente escrito para la Apple Macintosh de 512k en 1984-1985. Excel es una de las primeras planillas de cálculo en utilizar una interfaz gráfica con menús desplegables y la capacidad de clickear utilizando un puntero. Anteriormente se consideraba, que la planilla de cálculo Excel era para mucha gente más fácil que usar que el comando de interfaz de línea de los productos de PC-DOS.

3.2 Descripción del Programa

Un archivo de Microsoft Excel consta de un libro que contiene una o más hojas. Una hoja es como una hoja grande de contabilidad, con filas y columnas que se cruzan para formar celdas que guardan datos. Los datos pueden ser números o texto que pueden introducir fórmulas que calculan valores basados en referencias a otros números del libro.

La hoja de Microsoft Excel tiene una longitud de 16.384 filas y un ancho de 256 columnas.

3.3 Ventajas y características principales

• Es un programa de fácil manejo y muy potente, se realizan buenos trabajos, como puede ser una factura o bien nóminas o también llevar un control de los apuntes del banco, llevar las comisiones, los pagos, etc
• Los cálculos en este programa no son comparables porque mientras no se especifique lo contrario son exactos - en Excel son muy precisos.
• Excell incorpora un potente instrumento "El Solver". Este instrumento hace lo que los técnicos llaman "optimización": calcular el mejor valor de una función sometida a unas restricciones -o a ninguna-. Se pueden introducir muchas restricciones y la velocidad con las que calcula las soluciones es asombrosa.
• Una de las posibilidades de Excel es la de presentar los datos de forma estética: puedes ponerles varios tipos de bordes, usar varios tipos de letra...
• Puede utilizar hojas para almacenar datos numéricos
• Utilizar las órdenes y herramientas de Microsoft Excel para ejecutar cálculos con sus datos.
• Puede ordenar, reorganizar, analizar y presentar sus datos fácilmente utilizando las prestaciones de Microsoft Excel, como son la copia, el desplazamiento, la ordenación, la consolidación, la representación gráfica y las tablas dinámicas.
• Puede en Excel sumar filas y columnas.
• Puede crear fórmulas para realizar cálculos tan simples como sumar los valores de dos celdas, o tan complejos como encontrar la desviación de un valor concreto con respecto a un conjunto de valores.
• La utilización de las casillas del excel para realizar evaluaciones de una misma función con diferentes valores, es una de las características principales de este herramienta
• En excell podemos insertar y/o eliminar celdas, filas y columnas, diferente si trabajamos manualmente, ya que tendríamos que realizar el trabajo casi completo nuevamente si necesitaramos una fila o una columna.
• Podemos crear gráficos. Un gráfico es la representación gráfica de los datos de una hoja de cálculo facilitando de esta manera su interpretación. A la hora de crear un gráfico, Excel dispone de un asistente que nos guiará en la creación de éste. Puede crear gráficos de dos formas: en la misma hoja que sus datos o en una hoja de gráfico aparte en el mismo libro de trabajo.

OpenOffice.org Calc

OpenOffice.org Calc es una hoja de cálculo Open Source y software libre compatible con Microsoft Excel. Es parte de la suite ofimática OpenOffice.org. Como con todos los componentes de la suite OpenOffice.org, Calc puede usarse a través de una variedad de plataformas, incluyendo Mac OS X, Windows, GNU/Linux, FreeBSD y Solaris, y está disponible bajo licencia LGPL

GENERALIDADES:

Calc es una hoja de cálculo similar con un rango de características más o menos equivalente. Su tamaño es mucho menor y proporciona un número de características no presentes en Excel, incluyendo un sistema que automáticamente define series para representar gráficamente basado en la disposición de los datos del usuario. Calc también es capaz de exportar hojas de cálculo como archivos PDF, cuenta con filtros, autofiltros y además puede realizar agrupaciones en tablas dinámicas que Lotus 123 en sus versiones anteriores no hacía, posiblemente la versión 9.8 de Lotus 123 tenga estas posibilidades.

Dado que, desde el punto de vista de la programación de macros, Calc no es compatible con el modelo de objetos de Excel (aunque sí con prácticamente todo su repertorio de funciones BASIC), no es tan vulnerable a los virus de macros (o macrovirus) como el producto de Microsoft. Además, dado que su difusión es bastante menor, no hay tanto interés por parte de los creadores de software malicioso (malware) de atacarlo específicamente.

Calc puede abrir y guardar las hojas de cálculo en el formato de archivos de Microsoft Excel. El formato por defecto de OpenOffice.org 2.0 Calc se puede fijar para que sea el de Microsoft Excel, o el formato Open Document Format (ODF) de la organización OASIS. Calc también apoya una amplia gama de otros formatos, tanto para abrir y guardar archivos.

OpenOffice.org es software libre. Cualquier persona puede hacer mejoras y luego compartirlas para el disfrute de todos. A medida que continúa creciendo la base de usuarios y desarrolladores de OpenOffice.org, las características y mejoras pueden ser agregadas al paquete a mayor ritmo.

En algunos casos, Calc carece de asistentes para acceder a ciertas características avanzadas asociadas a productos de la competencia como capacidades estadísticas como el soporte de la barra de error en los gráficos, y el análisis de regresión polinómico, sin embargo esos cálculos se puede realizar incorporando manualmente las funciones y las relaciones más algunos macros. Otra aplicación FOSS llamada Gnumeric proporcionaría un acceso más fácil en estas características del análisis estadístico exponiéndolas a los usuarios con asistentes.

Crítica sobre el rendimiento

La versión 2.0 de Calc tenía problemas al manejar hojas de cálculo muy grandes (20.000 filas con 100 columnas). Esto es en parte debido al formato XML para manejar entradas en las celdas. Un hacker de Novell Linux y el GNOME, llamado Federico Mena Quintero, ha analizado la causa del retardo en su blog [1] y ofreció algunas sugerencias para mejorar la situación. Estas críticas se han disipado, ya que las versiones de Go-oo (http://www.go-oo.org), entre las que se encuentra la distribuida por Canonical en Ubuntu, permiten más de un millón de filas y 1.024 columnas.

La mayoría de los usuarios que trabajan con un conjunto de datos (datasets) tan grandes usan un programa manejador de bases de datos (como MySQL o PostgreSQL), así que no es un gran problema. En OpenOffice.org se puede conectar con bases de datos externas usando el componente Base.

Tipos de fórmulas en Calc

Aunque no sea una clasificación exacta, vamos a decir que Calc puede utilizar tres tipos distintos de fórmulas, dependiendo de los elementos que incluyamos en la expresión que introducimos tras el signo =.

Clasificaremos las fórmulas en los siguientes tipos:

• Fórmulas simples: Realizan operaciones simples con valores constantes, como si de una calculadora se tratase.

• Fórmulas con referencias: Realizan operaciones simples con referencias a otras celdas y opcionalmente con valores constantes, operando con el valor que éstas contienen. La referencia se indica introduciendo el nombre de la celda.

• Fórmulas con funciones: Realizar operaciones simples con referencias a otras celdas y opcionalmente con valores constantes, y además con otro tipo de expresiones llamados funciones. Veremos en el capítulo siguiente que son las funciones y como se incorporan a las fórmulas.

Por lo tanto, las fórmulas se insertan en una celda empezando por un signo = y a continuación una expresión formada por valores constantes (fechas, números, textos...), operadores (sumar, multiplicar, restar...), referencias a otras celdas o rangos (B5, H3:K12) y/u otro tipo de expresiones llamados funciones.

No son lo mismo fórmulas que funciones. Ambas son expresiones, pero son cosas distintas. Las segundas las trataremos ampliamente en los capítulos Las funciones y Funciones más habituales.

• Fórmulas simples
• Fórmulas con referencias
• Fórmulas con funciones

Comparación contra Microsoft Excel

 

Calc, al igual que el resto de la suite Open Office, puede fácilmente exportar hojas de cálculo (obviamente incluyendo gráficos) como archivo PDF a partir de su versión 1.1.0 (lanzada en marzo de 2004). En contraste, Excel sólo incluye esta característica desde su versión 2007.

Otra de las ventajas de Calc es que directamente usas medidas métricas cuando define el ancho de una celda o columna, o la altura de una celda o fila. Este número se puede expresar tanto en cm, mm, pulgadas, picas y puntos (tipográficos).

Asimismo Calc tiene algunas funciones adicionales, como DOMINGODEPASCUA, la cual trabaja casi con cualquier año. Otras como DÍAS y AÑOS (las cuales calculan diferencias entre fechas), se pueden reemplazar con la relativamente desconocida, y muy poco documentada SIFECHA de Excel (DATEDIF en inglés, llamada así en español debido a un error de traducción).1

No obstante, aunque Calc soporta totalmente el formato condicional de Excel 97-2003, no soporta las mejoras implementadas al mismo en la versión 2007 de Excel, así como tampoco, las "barras de datos" que se pueden asociar a celdas específicas.

Por otro lado, y a diferencia del producto de Microsoft (incluso su versión 2010), Calc ofrece un asistente de funciones más sofisticado, que le permite al usuario navegar a través de fórmulas anidadas.

Calc también permite fechas mucho menores que al primero de enero de 1900, la cual puede ser útil para calcular períodos históricos. Por ejemplo HOY()-FECHA(1789; 7; 14) devuelve la cantidad de días entre la fecha actual del sistema y la Toma de la Bastilla. Aún más, puede ir tan atrás como el primero de enero del año 100 (después de Cristo), compensando el desfase de 11 días debido al pasaje desde el calendario juliano al gregoriano (que tuvo lugar cuando se pasó, en los entonces países católicos, del 4 de octubre de 1582 al 15 del mismo mes y año). Este desplazamiento permite calcular correctamente que el día del "descubrimiento oficial" de América (12 de octubre de 1492) efectivamente cayó un día viernes (mediante la función DÍASEM o, eventualmente, usando MÓDULO).

Finalmente, respecto de las macros, las funciones de BASIC de Calc son básicamente las mismas que las de Excel, aunque al primero le suelen faltar algunas, como InStrRev (la cual busca una subcadena en una cadena, recorriéndola en reversa, desde atrás hacia adelante). Pero desafortunadamente, el modelo de objetos de Calc es bastante diferente del de Excel, y no soporta la característica de "edición inteligente" del producto de Microsoft, heredada del entorno de programación Visual Studio, relacionada al manejo fácil de cada objecto.propiedad u objeto.procedimiento (objeto.método).

Fórmulas

Las fórmulas son ecuaciones que efectúan cálculos con los valores de la hoja de cálculo. Una fórmula comienza por un signo igual (=). Por ejemplo, la siguiente fórmula multiplica 2 por 3 y, a continuación, suma 5 al resultado.

=5+2*3

Una fórmula también puede contener lo siguiente: funciones (función: fórmula ya escrita que toma un valor o valores, realiza una operación y devuelve un valor o valores. Utilice funciones para simplificar y acortar fórmulas en una hoja de cálculo, especialmente aquellas que llevan a cabo cálculos prolongados o complejos.), referencias, operadores (operador: signo o símbolo que especifica el tipo de cálculo que se debe llevar a cabo en una expresión. Hay operadores matemáticos, comparativos, lógicos y referenciales.) y constantes (constante: valor que no ha sido calculado y que, por tanto, no varía. Por ejemplo, el número 210 y el texto "Ingresos trimestrales" son constantes. Las expresiones, o los valores resultantes de ellas, no son constantes.).

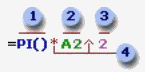
Partes de una fórmula

• Funciones: la función PI() devuelve el valor de pi: 3,142...
• Referencias (o nombres): A2 devuelve el valor de la celda A2.
• Constantes: números o valores de texto escritos directamente en una fórmula, por ejemplo, 2.
• Operadores: el operador ^ (acento circunflejo) eleva un número a una potencia, y el operador * (asterisco) multiplica.

Funciones en las fórmulas

Las funciones son fórmulas predefinidas que ejecutan cálculos utilizando valores específicos, denominados argumentos, en un orden determinado o estructura. Las funciones pueden utilizarse para ejecutar operaciones simples o complejas. Por ejemplo, la función REDONDEAR redondea un número en la celda A10.

Nombres en las fórmulas

Puede utilizar los rótulos de las columnas y filas de una hoja de cálculo para hacer referencia a las celdas de esas columnas o filas. También puede crear nombres (nombre: palabra o cadena de caracteres que representa una celda, rango de celdas, fórmula o valor constante. Utilice nombres fáciles de entender, como Productos, para referirse a rangos difíciles de entender, como Ventas!C20:C30.) descriptivos para representar las celdas, los rangos de celdas, las fórmulas o los valores constantes (constante: valor que no ha sido calculado y que, por tanto, no varía. Por ejemplo, el número 210 y el texto "Ingresos trimestrales" son constantes. Las expresiones, o los valores resultantes de ellas, no son constantes.). Es posible utilizar rótulos en las fórmulas que hagan referencia a datos de la misma hoja de cálculo; si desea representar un rango en otra hoja, utilice un nombre.

Utilizar nombres definidos para representar celdas, constantes o fórmulas

Un nombre definido en una fórmula puede facilitar la comprensión del objetivo de la fórmula. Por ejemplo, la fórmula =SUMA(VentasPrimerTrimestre) puede ser más sencilla de identificar que =SUMA(C20:C30). Los nombres están disponibles en cualquier hoja de cálculo. Por ejemplo, si el nombre VentasProyectadas hace referencia al rango A20:A30 en la primera hoja del cálculo de un libro, puede utilizarse el nombre VentasProyectadas en cualquier hoja del mismo libro para hacer referencia al rango A20:A30 en la primera hoja de cálculo.

Los nombres también pueden utilizarse para representar fórmulas o valores que no cambien (constantes). Por ejemplo, puede utilizarse el nombre IVA para representar el importe del impuesto (como un porcentaje) aplicado a las transacciones de ventas.

También puede vincularlo a un nombre definido en otro libro, o definir un nombre que haga referencia a celdas de otro libro. Por ejemplo, la fórmula =SUMA(Ventas.xls!VentasProyectadas) hace referencia al rango con el nombre VentasProyectadas del libro denominado Ventas.

Nota  De forma predeterminada, en los nombres se utilizan referencias absolutas de celda (referencia de celda absoluta: en una fórmula, dirección exacta de una celda, independientemente de la posición de la celda que contiene la fórmula. Una referencia de celda absoluta tiene la forma $A$1.).

Caracteres permitidos   El primer carácter de un nombre deberá ser una letra o un carácter de subrayado. Los demás caracteres del nombre pueden ser letras, números, puntos y caracteres de subrayado.

Nombres iguales que referencias   Los nombres no pueden ser iguales que una referencia de celda, como Z$100 o L1C1.

Usar varias palabras   Se pueden usar varias palabras pero no se permiten espacios. Pueden utilizarse caracteres de subrayado y puntos como separadores de palabras; por ejemplo, Impuesto_Ventas o Primer.Trimestre.

Número de caracteres permitido   Un nombre puede contener 255 caracteres como máximo.

Nota  Si un nombre definido para un rango contiene más de 253 caracteres, no podrá seleccionarlo en el cuadro Nombre.

Distinción entre mayúsculas y minúsculas   Los nombres pueden contener letras mayúsculas y minúsculas. Microsoft Excel no distingue entre mayúsculas y minúsculas en los nombres. Por ejemplo, si se ha creado el nombre Ventas y, se crea otro denominado VENTAS en el mismo libro, el segundo nombre reemplazará al primero.

Utilizar rótulos de filas y columnas existentes como nombres

Cuando se crea una fórmula que hace referencia a datos en una hoja de cálculo, se pueden utilizar los rótulos de fila y de columna de la hoja para hacer referencia a datos. Por ejemplo, para calcular el valor total de la columna Producto, utilice la fórmula =SUMA(Producto).

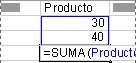
Utilizar un rótulo Si tiene que hacer referencia a la cantidad de Producto 3 correspondiente a la división Este (es decir, al valor 110,00), puede utilizar la fórmula =Producto 3 Este. El espacio que hay en la fórmula "Producto 3" y "Este" es el operador (operador: signo o símbolo que especifica el tipo de cálculo que se debe llevar a cabo en una expresión. Hay operadores matemáticos, comparativos, lógicos y referenciales.) de intersección. Este operador designa que Microsoft Excel debe buscar y devolver el valor de la celda en la intersección de la fila que tiene el rótulo Este y la columna que tiene el rótulo

Nota  De manera predeterminada, Excel no reconoce los rótulos de las fórmulas. Para utilizar rótulos en las fórmulas, haga clic en el comando Opciones del menú Herramientas y, a continuación, en la ficha Calcular. En Opciones del libro, active la casilla de verificación Aceptar rótulos en las fórmulas.

Rótulos apilados: Si utiliza rótulos para las columnas y filas en la hoja de cálculo, pueden utilizarlos para crear fórmulas que hagan referencia a los datos de la hoja de cálculo. Si la hoja de cálculo contiene rótulos de columna apilados  (un rótulo en una celda va seguido de uno o más rótulos por debajo de él),  pueden utilizarse en las fórmulas para hacer referencia a los datos de la hoja de cálculo. Por ejemplo, si el rótulo Oeste está en la celda E5 y el rótulo Previstas está en la celda E6, la fórmula =SUMA(Oeste Previstas) devolverá el valor total de la columna Oeste Previstas.

Orden de los rótulos apilados: Si se hace referencia a la información mediante el uso de rótulos apilados, la referencia se hará en el orden en que aparezcan los rótulos, de arriba a abajo. Si el rótulo Oeste está en la celda F5 y el rótulo Real está en la celda F6, puede hacer referencia a los números reales de Oeste mediante el uso de Oeste Real en una fórmula. Por ejemplo, para calcular el promedio de las cifras reales de Oeste, utilice la fórmula =PROMEDIO(Oeste Real).

Utilizar fechas como rótulos: Si se asigna un rótulo a un rango mediante el cuadro de diálogo Rango de rótulos y el rango contiene un año o una fecha como un rótulo, Excel definirá la fecha como un rótulo encerrándolo entre comillas sencillas cuando se escriba en una fórmula. Por ejemplo, supongamos que la hoja de cálculo contiene los rótulos 2007 y 2008 y que éstos se han especificado mediante el cuadro de diálogo Rango de rótulos. Cuando escriba la fórmula =SUMA(2008), Excel actualizará automáticamente la fórmula a =SUMA('2008').

Operaciones aritméticas básicas en plantillas de cálculo

Cada vez que se insertan datos en una celda, es posible observar que, por ejemplo, los datos literales o de texto se alinean a la izquierda de la celda mientras que un dato tipo numérico (entero o con decimales) se alinea a la derecha de la celda de forma automática.

Sin embargo, puede decirse que cada vez que se necesita hacer uno o más cálculos en una celda, es necesario escribir el cálculo de un modo diferente.

Existen operadores aritméticos básicos como la suma, la diferencia, el producto y el cociente que permiten realizar dichos cálculos, existen además funciones predeterminadas para dicho fin. En todos los casos, debe anteponerse el signo igual (=) a todos estos tipos de cálculos para que la plantilla “reconozca” a ese dato como una operación aritmética o función sobre determinado dato o grupo de datos.

Las cuatro operaciones básicas en plantillas: Suma, resta, producto y cociente

La multiplicación se realiza por medio del operador *. Por ejemplo =b1*c3, multiplica los valores que hay en las celdas b1 y c3. Se pueden multiplicar más de dos celdas.

La división se realiza por medio del operador /. Por ejemplo =b1/c3, divide el valor que hay en la celda b1 por el de la celda c3.

Si se desea elevar el valor de una celda al exponente n, debe utilizarse el símbolo circunflejo (^). Por ejemplo, para elevar el contenido de la celda c4 al cubo se escribe la fórmula =c4^3.

Si la suma es de pocas celdas, conviene sumarlas directamente: =a1+a2+a3. Lo mismo puede hacerse si necesita restarse: =a1-b1-c1.

Símbolos de agrupación de operaciones

Cuando se deben hacer operaciones combinadas (divisiones que se suman a una multiplicación, por ejemplo), se pueden usar paréntesis como en matemática para separar una operación de otra. Sin embargo, y también del mismo modo que en matemática, las operaciones tienen un Orden de Prioridad “natural” de operación. Primero se resuelven potencias y raíces. Después cocientes y productos.

Orden de prioridad de las operaciones

Todas las subexpresiones entre paréntesis se evalúan primero. Las subexpresiones con paréntesis anidados se evalúan desde el centro hacia los extremos.

Dentro de una expresión, los operadores se evalúan de la siguiente manera:

° Se analiza la expresión de izquierda a derecha.

° Si en la expresión existen paréntesis, lo que se encuentra dentro de estos se evalúan de izquierda a derecha según orden de prioridad de los mismos.

° Si en la expresión se encuentran más de un par de paréntesis, la evaluación se realiza comenzando con el paréntesis que se encuentra más a la izquierda en la expresión hasta llegar al par de paréntesis que se encuentra más a la derecha de la expresión.

Nociones de constantes y variables

Un par de conceptos de vital interés en matemática, y en toda aplicación de esta ciencia a un área específica de conocimiento, es el de constante y variable. Para emplear una terminología simple, entenderemos por constante todo número (o más genéricamente todo valor) conciso.

Una variable en cambio, y como su nombre lo sugiere, es una representación de un dato que puede no tener el mismo valor siempre.

Así, cuando decimos La temperatura de ebullición del agua es de 100º C, estamos haciendo referencia a un valor constante para ese fenómeno en particular. Sin embargo si hacemos referencia a la experiencia de calentar el agua, observaremos que a medida que transcurre el tiempo, los valores que toma la temperatura van variando hasta alcanzar la ebullición. En este segundo caso, a la temperatura se la considera variable.

Operaciones con constantes

La plantilla de cálculo Excel, por supuesto, puede manipular de forma directa valores específicos (constantes), de modo similar a una calculadora.

Así, si se desean sumar los números 12, 13, 12 y 14 que están en las celdas a1, a2, a3 y a4 respectivamente, será suficiente con posicionarse, por ejemplo, en la celda a5 y escribir =12+13+12+14.

Como se verá a continuación, esta forma de realizar cálculos (complejos o no), no es recomendable. Cometer un error en la carga de un valor implicaría corregir el número erróneo, y además la fórmula en sí misma.

Operaciones con variables. Ventajas

Puede añadirse a todo lo anteriormente expuesto que en Ciencias de la Computación, la interpretación de constante y de variable es similar a la de matemática, pero tiene además un enfoque particular en lo referente a la idea de variable.

Se considera que toda variable, en informática, almacena un valor. De este modo será mucho más ventajoso manipular una variable, y no su contenido específico. En la Planilla de Cálculo Excel, manipular variables equivale a manipular celdas.

De este modo, en el ejemplo anterior, será más eficiente escribir en la celda a5 la fórmula “con variables” =a1+a2+a3+a4, que la fórmula “con constantes” =12+13+12+14. En la primera, si se comete un error al cargar los valores de a1 a a4, solamente se corregirá/n dicho/s error/es. Como la fórmula está escrita “en celdas” – o sea manipulando variables – la fórmula en sí misma recalculará el resultado correcto sin necesidad de ser corregida.

Una fórmula es una secuencia formada por valores constantes, referencias a otras celdas, nombres, funciones, u operadores. Una fórmula es una técnica básica para el análisis de datos. Se pueden realizar diversas operaciones con los datos de las hojas de cálculo como *, +, -, Seno, Coseno, etc... En una fórmula se pueden mezclar constantes, nombres, referencias a otras celdas, operadores y funciones. La fórmula se escribe en la barra de fórmulas y debe empezar siempre por el signo =.

Los distintos tipos de operadores que se pueden utilizar en una fórmula son : Operadores aritméticos se emplean para producir resultados numéricos. Ejemplo: + - * /  % ^ Operador tipo texto se emplea para concatenar celdas que contengan texto. Ejemplo: & Operadores relacionales se emplean para comparar valores y proporcionar un valor lógico (verdadero o falso) como resultado de la comparación. Ejemplo: < > = <= >= <> Operadores de referencia indican que el valor producido en la celda referenciada debe ser utilizado en la fórmula. En Excel pueden ser: - Operador de rango indicado por dos puntos (:), se emplea para indicar un rango de celdas. Ejemplo: A1:G5 - Operador de unión indicado por una coma (,), une los valores de dos o más celdas. Ejemplo: A1,G5

Cuando hay varias operaciones en una misma expresión, cada parte de la misma se evalúa y se resuelve en un orden determinado. Ese orden se conoce como prioridad de los operadores. Se pueden utilizar paréntesis para modificar el orden de prioridad y forzar la resolución de algunas partes de una expresión antes que otras.

Las operaciones entre paréntesis son siempre ejecutadas antes que las que están fuera del paréntesis. Sin embargo, dentro de los paréntesis se mantiene la prioridad normal de los operadores. Cuando hay expresiones que contienen operadores de más de una categoría, se resuelve antes las que tienen operadores aritméticos, a continuación las que tienen operadores de comparación y por último las de operadores lógicos .

Los operadores de comparación tienen todos la misma prioridad, es decir que son resueltos de izquierda a derecha, en el orden en que aparecen. Son: Comparación Igualdad (=) Desigualdad (<>) Menor que (<) Mayor que (>) Menor o igual que (<=) Mayor o igual que (>=)

Los operadores lógicos y aritméticos son resueltos en el siguiente orden de prioridad (de mayor a menor): Aritméticos Lógicos Exponenciación (^) Not Negación (-) And Multiplicación (*) y División (/) Or Adición (+) y Sustracción (-) Concatenación de caracteres (&) Cuando hay multiplicación y división en la misma expresión, cada operación es resuelta a medida que aparece, de izquierda a derecha. Del mismo modo, cuando se presentan adiciones y sustracciones en una misma expresión, cada operación es resuelta en el orden en que aparece, de izquierda a derecha. El operador de concatenación de cadenas de caracteres (&) no es realmente un operador aritmético pero es prioritario respecto a todos los operadores de comparación.

Funciones Una función es una fórmula especial escrita con anticipación y que acepta un valor o valores, realiza unos cálculos con esos valores y devuelve un resultado. Todas las funciones tienen que seguir una sintaxis y si ésta no se respeta Excel nos mostrará un mensaje de error. 1) Los argumentos o valores de entrada van siempre entre paréntesis. No dejes espacios antes o después de cada paréntesis. 2) Los argumentos pueden ser valores constantes (número o texto), fórmulas o funciones. 3) Los argumentos deben de separarse por un punto y coma ";". Ejemplo: =SUMA(A1:B3) esta función equivale a =A1+A2+A3+B1+B2+B3

Referencias relativas

Cuando escribimos una fórmula, cualquiera que sea, podemos evitar escribirla muchas veces por medio del punto de autorellenado, que está en la celda seleccionada abajo a la derecha. Si nos ubicamos en la celda que contiene la fórmula, y acercamos el ratón a ese punto hasta que el puntero se transforma en una cruz finita y negra, puede apretarse el botón sin soltarse y "arrastrar" la fórmula al resto de las celdas. Cuando esto se hace de arriba para abajo, el número de la fila de la celda inicial se va incrementando en uno, y la letra de la columna queda fija. O sea que si la primera celda (la que contenía la fórmula), era c2, el autollenado celda por celda va siendo c3, c4, c5,…, c7, (suponiendo que la última sea c7). Si lo mismo se hace, por ejemplo, de izquierda a derecha, ocurre al revés. El número de la fila queda fijo, pero aumenta en uno la letra de la columna. O sea que si la primera celda (la que contenía la fórmula), era c2, el autollenado celda por celda va siendo d2, e2, f2,…, j2, (suponiendo que la última sea j2).

Referencias absolutas

Muchas veces ocurre que un valor en una celda debe afectar a varios valores que se encuentran en otro grupo de celdas. Por ejemplo, en una celda puede haber un precio que debe multiplicar a varias cantidades que se encuentran en otras celdas; o un porcentaje (de descuento o de incremento) debe multiplicar a varios importes que están en otro rango de celdas. Para poder utilizar la celda de precios, por ejemplo, para realizar las multiplicaciones, no podríamos autollenar la fórmula de multiplicación para todas las celdas. ¿Por qué?, porque como el número de la fila aumenta (es relativa), ya la celda del precio no multiplicaría a todos los números. Entonces, cuando se tiene que multiplicar un número en una celda por varios números que están en otras celdas, lo que conviene es inmovilizar la celda que contiene el precio. Esto se llama hacer una celda o referencia absoluta. Hay dos maneras de hacer esto. La primera es colocar el cursor (con el mouse o las teclas de dirección) delante de la celda que se quiere inmovilizar y pulsar la tecla F4. Supongamos que nuestro precio se encuentra en la celda b1 y la deseamos multiplicar por una primera cantidad de artículos que está en la celda c5. Cuando escribamos esa primera fórmula quedará =b1*c5. Para inmovilizar la celda b1 que tiene el precio por artículo, colocamos el cursor delante de la celda b1 (es decir entre el signo "=" y la "b" de b1) y después de pulsar la tecla F4, la fórmula quedará: =$b$1*c5, con lo cual ya la celda b1 está inmovilizada y al autollenar, no se modificará ni la letra "b" de la columna, ni el número 1 de la fila. Hecho esto, todos los números c5, c6, c7,…. Quedarán multiplicados por lo que hay en b1.

La otra manera de hacerlo es directamente tipear el signo $ delante de la b y el mismo signo delante del número 1 al escribir la fórmula. Del mismo modo anterior, la fórmula se podrá autollenar al resto de las celdas.

Ordenamiento de datos

Si lo que se desea es ordenar un conjunto de datos, debe seleccionarse el mismo (inclusive los rótulos) y puede ordenarse directamente en base a la primera columna (columna A), utilizando los botones A-Z (ascendente) o Z-A (descendente). Si se quiere ordenar por alguna otra columna que no sea la primera (la A), hay que seleccionar todos los datos (con rótulos y todo) e ir a DATOS y elegir la opción Ordenar… En el cuadro que aparece, arriba de todo permite elegir de una lista desplegable por cuál rótulo de columna quere ser la primera también), y a la derecha aparece si queremos que el ordenamiento sea ascendente o descendente.

 

PLANTILLAS DE CALCULO

INTRODUCCIÓN

El uso de una computadora ha llegado a evolucionar el trabajo, tal es el caso de trabajar en hojas de cálculo para agilizar tareas contables, financieras, matemáticas...

Se le asigna el nombre de hoja de cálculo a un hoja que esta divida en renglones y columnas, al cruce de ellos se le denomina celdas sobre las cuales se almacena información (letras o números) que podemos usar para realizar operaciones, tales como sumas, restas, multiplicaciones, divisiones, cálculos financieros, estadisticos, de ingeniería, amortizaciones, etc.

Por su parte, las hojas de cálculo no son simples celdas para introducir números con los que realizar diferentes operaciones: son herramientas que permiten tratar esos números y hacer gráficos o exportarlos a otros documentos.

I. PLANILLAS DE CALCULO

Las planillas de cálculos electrónicas o computarizadas son de origen mucho reciente. Muchas revistas le otorgan a Dan Bricklin el título de "padre" de las planillas de cálculo electrónicas.

1.1 Definición

Una planilla de cálculo es un programa que permite a los usuarios realizar tareas sin hacer ningún tipo de programación.

Cada celda de esta planilla, puede contener 3 tipos de entradas:

• Información numérica, por ejemplo números;
• Información alfabética o alfanumérica (palabras, letras, caracteres, números no utilizados en un cálculo) y
• Columnas con fórmulas, usualmente comenzadas con letras de celdas.

1.2 Usos

Usos generales de las planillas de cálculo:

• Almacenamiento de datos;
• Cálculos completos, por ejemplo presupuestos;
• Aplicaciones en matemática (teoremas, graficando funciones polinominales, aproximación de raíces irracionales, hipótesis); comparaciones, estadísticas, encuestas… 

OpenOffice.org Calc

OpenOffice.org Calc es una hoja de cálculo Open Source y software libre compatible con Microsoft Excel. Es parte de la suite ofimática OpenOffice.org. Como con todos los componentes de la suite OpenOffice.org, Calc puede usarse a través de una variedad de plataformas, incluyendo Mac OS X, Windows, GNU/Linux, FreeBSD y Solaris, y está disponible bajo licencia LGPL

GENERALIDADES:

Calc es una hoja de cálculo similar con un rango de características más o menos equivalente. Su tamaño es mucho menor y proporciona un número de características no presentes en Excel, incluyendo un sistema que automáticamente define series para representar gráficamente basado en la disposición de los datos del usuario. Calc también es capaz de exportar hojas de cálculo como archivos PDF, cuenta con filtros, autofiltros y además puede realizar agrupaciones en tablas dinámicas que Lotus 123 en sus versiones anteriores no hacía, posiblemente la versión 9.8 de Lotus 123 tenga estas posibilidades.

Dado que, desde el punto de vista de la programación de macros, Calc no es compatible con el modelo de objetos de Excel (aunque sí con prácticamente todo su repertorio de funciones BASIC), no es tan vulnerable a los virus de macros (o macrovirus) como el producto de Microsoft. Además, dado que su difusión es bastante menor, no hay tanto interés por parte de los creadores de software malicioso (malware) de atacarlo específicamente.

Calc puede abrir y guardar las hojas de cálculo en el formato de archivos de Microsoft Excel. El formato por defecto de OpenOffice.org 2.0 Calc se puede fijar para que sea el de Microsoft Excel, o el formato Open Document Format (ODF) de la organización OASIS. Calc también apoya una amplia gama de otros formatos, tanto para abrir y guardar archivos.

OpenOffice.org es software libre. Cualquier persona puede hacer mejoras y luego compartirlas para el disfrute de todos. A medida que continúa creciendo la base de usuarios y desarrolladores de OpenOffice.org, las características y mejoras pueden ser agregadas al paquete a mayor ritmo.

En algunos casos, Calc carece de asistentes para acceder a ciertas características avanzadas asociadas a productos de la competencia como capacidades estadísticas como el soporte de la barra de error en los gráficos, y el análisis de regresión polinómico, sin embargo esos cálculos se puede realizar incorporando manualmente las funciones y las relaciones más algunos macros. Otra aplicación FOSS llamada Gnumeric proporcionaría un acceso más fácil en estas características del análisis estadístico exponiéndolas a los usuarios con asistentes.

Crítica sobre el rendimiento

La versión 2.0 de Calc tenía problemas al manejar hojas de cálculo muy grandes (20.000 filas con 100 columnas). Esto es en parte debido al formato XML para manejar entradas en las celdas. Un hacker de Novell Linux y el GNOME, llamado Federico Mena Quintero, ha analizado la causa del retardo en su blog [1] y ofreció algunas sugerencias para mejorar la situación. Estas críticas se han disipado, ya que las versiones de Go-oo (http://www.go-oo.org), entre las que se encuentra la distribuida por Canonical en Ubuntu, permiten más de un millón de filas y 1.024 columnas.

La mayoría de los usuarios que trabajan con un conjunto de datos (datasets) tan grandes usan un programa manejador de bases de datos (como MySQL o PostgreSQL), así que no es un gran problema. En OpenOffice.org se puede conectar con bases de datos externas usando el componente Base.

Tipos de fórmulas en Calc

Aunque no sea una clasificación exacta, vamos a decir que Calc puede utilizar tres tipos distintos de fórmulas, dependiendo de los elementos que incluyamos en la expresión que introducimos tras el signo =.

Clasificaremos las fórmulas en los siguientes tipos:

• Fórmulas simples: Realizan operaciones simples con valores constantes, como si de una calculadora se tratase.

• Fórmulas con referencias: Realizan operaciones simples con referencias a otras celdas y opcionalmente con valores constantes, operando con el valor que éstas contienen. La referencia se indica introduciendo el nombre de la celda.

• Fórmulas con funciones: Realizar operaciones simples con referencias a otras celdas y opcionalmente con valores constantes, y además con otro tipo de expresiones llamados funciones. Veremos en el capítulo siguiente que son las funciones y como se incorporan a las fórmulas.

Por lo tanto, las fórmulas se insertan en una celda empezando por un signo = y a continuación una expresión formada por valores constantes (fechas, números, textos...), operadores (sumar, multiplicar, restar...), referencias a otras celdas o rangos (B5, H3:K12) y/u otro tipo de expresiones llamados funciones.

No son lo mismo fórmulas que funciones. Ambas son expresiones, pero son cosas distintas. Las segundas las trataremos ampliamente en los capítulos Las funciones y Funciones más habituales.

• Fórmulas simples
• Fórmulas con referencias
• Fórmulas con funciones

Comparación contra Microsoft Excel

Calc, al igual que el resto de la suite Open Office, puede fácilmente exportar hojas de cálculo (obviamente incluyendo gráficos) como archivo PDF a partir de su versión 1.1.0 (lanzada en marzo de 2004). En contraste, Excel sólo incluye esta característica desde su versión 2007.

Otra de las ventajas de Calc es que directamente usas medidas métricas cuando define el ancho de una celda o columna, o la altura de una celda o fila. Este número se puede expresar tanto en cm, mm, pulgadas, picas y puntos (tipográficos).

Asimismo Calc tiene algunas funciones adicionales, como DOMINGODEPASCUA, la cual trabaja casi con cualquier año. Otras como DÍAS y AÑOS (las cuales calculan diferencias entre fechas), se pueden reemplazar con la relativamente desconocida, y muy poco documentada SIFECHA de Excel (DATEDIF en inglés, llamada así en español debido a un error de traducción).1

No obstante, aunque Calc soporta totalmente el formato condicional de Excel 97-2003, no soporta las mejoras implementadas al mismo en la versión 2007 de Excel, así como tampoco, las "barras de datos" que se pueden asociar a celdas específicas.

Por otro lado, y a diferencia del producto de Microsoft (incluso su versión 2010), Calc ofrece un asistente de funciones más sofisticado, que le permite al usuario navegar a través de fórmulas anidadas.

Calc también permite fechas mucho menores que al primero de enero de 1900, la cual puede ser útil para calcular períodos históricos. Por ejemplo HOY()-FECHA(1789; 7; 14) devuelve la cantidad de días entre la fecha actual del sistema y la Toma de la Bastilla. Aún más, puede ir tan atrás como el primero de enero del año 100 (después de Cristo), compensando el desfase de 11 días debido al pasaje desde el calendario juliano al gregoriano (que tuvo lugar cuando se pasó, en los entonces países católicos, del 4 de octubre de 1582 al 15 del mismo mes y año). Este desplazamiento permite calcular correctamente que el día del "descubrimiento oficial" de América (12 de octubre de 1492) efectivamente cayó un día viernes (mediante la función DÍASEM o, eventualmente, usando MÓDULO).

Finalmente, respecto de las macros, las funciones de BASIC de Calc son básicamente las mismas que las de Excel, aunque al primero le suelen faltar algunas, como InStrRev (la cual busca una subcadena en una cadena, recorriéndola en reversa, desde atrás hacia adelante). Pero desafortunadamente, el modelo de objetos de Calc es bastante diferente del de Excel, y no soporta la característica de "edición inteligente" del producto de Microsoft, heredada del entorno de programación Visual Studio, relacionada al manejo fácil de cada objecto.propiedad u objeto.procedimiento (objeto.método).

Fórmulas

Las fórmulas son ecuaciones que efectúan cálculos con los valores de la hoja de cálculo. Una fórmula comienza por un signo igual (=). Por ejemplo, la siguiente fórmula multiplica 2 por 3 y, a continuación, suma 5 al resultado.

=5+2*3

Una fórmula también puede contener lo siguiente: funciones (función: fórmula ya escrita que toma un valor o valores, realiza una operación y devuelve un valor o valores. Utilice funciones para simplificar y acortar fórmulas en una hoja de cálculo, especialmente aquellas que llevan a cabo cálculos prolongados o complejos.), referencias, operadores (operador: signo o símbolo que especifica el tipo de cálculo que se debe llevar a cabo en una expresión. Hay operadores matemáticos, comparativos, lógicos y referenciales.) y constantes (constante: valor que no ha sido calculado y que, por tanto, no varía. Por ejemplo, el número 210 y el texto "Ingresos trimestrales" son constantes. Las expresiones, o los valores resultantes de ellas, no son constantes.).

Partes de una fórmula

• Funciones: la función PI() devuelve el valor de pi: 3,142...
• Referencias (o nombres): A2 devuelve el valor de la celda A2.
• Constantes: números o valores de texto escritos directamente en una fórmula, por ejemplo, 2.
• Operadores: el operador ^ (acento circunflejo) eleva un número a una potencia, y el operador * (asterisco) multiplica.

Funciones en las fórmulas

Las funciones son fórmulas predefinidas que ejecutan cálculos utilizando valores específicos, denominados argumentos, en un orden determinado o estructura. Las funciones pueden utilizarse para ejecutar operaciones simples o complejas. Por ejemplo, la función REDONDEAR redondea un número en la celda A10.

Nombres en las fórmulas

Puede utilizar los rótulos de las columnas y filas de una hoja de cálculo para hacer referencia a las celdas de esas columnas o filas. También puede crear nombres (nombre: palabra o cadena de caracteres que representa una celda, rango de celdas, fórmula o valor constante. Utilice nombres fáciles de entender, como Productos, para referirse a rangos difíciles de entender, como Ventas!C20:C30.) descriptivos para representar las celdas, los rangos de celdas, las fórmulas o los valores constantes (constante: valor que no ha sido calculado y que, por tanto, no varía. Por ejemplo, el número 210 y el texto "Ingresos trimestrales" son constantes. Las expresiones, o los valores resultantes de ellas, no son constantes.). Es posible utilizar rótulos en las fórmulas que hagan referencia a datos de la misma hoja de cálculo; si desea representar un rango en otra hoja, utilice un nombre.

Utilizar nombres definidos para representar celdas, constantes o fórmulas

Un nombre definido en una fórmula puede facilitar la comprensión del objetivo de la fórmula. Por ejemplo, la fórmula =SUMA(VentasPrimerTrimestre) puede ser más sencilla de identificar que =SUMA(C20:C30). Los nombres están disponibles en cualquier hoja de cálculo. Por ejemplo, si el nombre VentasProyectadas hace referencia al rango A20:A30 en la primera hoja del cálculo de un libro, puede utilizarse el nombre VentasProyectadas en cualquier hoja del mismo libro para hacer referencia al rango A20:A30 en la primera hoja de cálculo.

Los nombres también pueden utilizarse para representar fórmulas o valores que no cambien (constantes). Por ejemplo, puede utilizarse el nombre IVA para representar el importe del impuesto (como un porcentaje) aplicado a las transacciones de ventas.

También puede vincularlo a un nombre definido en otro libro, o definir un nombre que haga referencia a celdas de otro libro. Por ejemplo, la fórmula =SUMA(Ventas.xls!VentasProyectadas) hace referencia al rango con el nombre VentasProyectadas del libro denominado Ventas.

Nota  De forma predeterminada, en los nombres se utilizan referencias absolutas de celda (referencia de celda absoluta: en una fórmula, dirección exacta de una celda, independientemente de la posición de la celda que contiene la fórmula. Una referencia de celda absoluta tiene la forma $A$1.).

Caracteres permitidos   El primer carácter de un nombre deberá ser una letra o un carácter de subrayado. Los demás caracteres del nombre pueden ser letras, números, puntos y caracteres de subrayado.

Nombres iguales que referencias   Los nombres no pueden ser iguales que una referencia de celda, como Z$100 o L1C1.

Usar varias palabras   Se pueden usar varias palabras pero no se permiten espacios. Pueden utilizarse caracteres de subrayado y puntos como separadores de palabras; por ejemplo, Impuesto_Ventas o Primer.Trimestre.

Número de caracteres permitido   Un nombre puede contener 255 caracteres como máximo.

Nota  Si un nombre definido para un rango contiene más de 253 caracteres, no podrá seleccionarlo en el cuadro Nombre.

Distinción entre mayúsculas y minúsculas   Los nombres pueden contener letras mayúsculas y minúsculas. Microsoft Excel no distingue entre mayúsculas y minúsculas en los nombres. Por ejemplo, si se ha creado el nombre Ventas y, se crea otro denominado VENTAS en el mismo libro, el segundo nombre reemplazará al primero.

Utilizar rótulos de filas y columnas existentes como nombres

Cuando se crea una fórmula que hace referencia a datos en una hoja de cálculo, se pueden utilizar los rótulos de fila y de columna de la hoja para hacer referencia a datos. Por ejemplo, para calcular el valor total de la columna Producto, utilice la fórmula =SUMA(Producto).

Utilizar un rótulo Si tiene que hacer referencia a la cantidad de Producto 3 correspondiente a la división Este (es decir, al valor 110,00), puede utilizar la fórmula =Producto 3 Este. El espacio que hay en la fórmula "Producto 3" y "Este" es el operador (operador: signo o símbolo que especifica el tipo de cálculo que se debe llevar a cabo en una expresión. Hay operadores matemáticos, comparativos, lógicos y referenciales.) de intersección. Este operador designa que Microsoft Excel debe buscar y devolver el valor de la celda en la intersección de la fila que tiene el rótulo Este y la columna que tiene el rótulo

Nota  De manera predeterminada, Excel no reconoce los rótulos de las fórmulas. Para utilizar rótulos en las fórmulas, haga clic en el comando Opciones del menú Herramientas y, a continuación, en la ficha Calcular. En Opciones del libro, active la casilla de verificación Aceptar rótulos en las fórmulas.

Rótulos apilados: Si utiliza rótulos para las columnas y filas en la hoja de cálculo, pueden utilizarlos para crear fórmulas que hagan referencia a los datos de la hoja de cálculo. Si la hoja de cálculo contiene rótulos de columna apilados  (un rótulo en una celda va seguido de uno o más rótulos por debajo de él),  pueden utilizarse en las fórmulas para hacer referencia a los datos de la hoja de cálculo. Por ejemplo, si el rótulo Oeste está en la celda E5 y el rótulo Previstas está en la celda E6, la fórmula =SUMA(Oeste Previstas) devolverá el valor total de la columna Oeste Previstas.

Orden de los rótulos apilados: Si se hace referencia a la información mediante el uso de rótulos apilados, la referencia se hará en el orden en que aparezcan los rótulos, de arriba a abajo. Si el rótulo Oeste está en la celda F5 y el rótulo Real está en la celda F6, puede hacer referencia a los números reales de Oeste mediante el uso de Oeste Real en una fórmula. Por ejemplo, para calcular el promedio de las cifras reales de Oeste, utilice la fórmula =PROMEDIO(Oeste Real).

Utilizar fechas como rótulos: Si se asigna un rótulo a un rango mediante el cuadro de diálogo Rango de rótulos y el rango contiene un año o una fecha como un rótulo, Excel definirá la fecha como un rótulo encerrándolo entre comillas sencillas cuando se escriba en una fórmula. Por ejemplo, supongamos que la hoja de cálculo contiene los rótulos 2007 y 2008 y que éstos se han especificado mediante el cuadro de diálogo Rango de rótulos. Cuando escriba la fórmula =SUMA(2008), Excel actualizará automáticamente la fórmula a =SUMA('2008').

EL PODER DE LA HOJA DE CALCULO

Introducción

En estos tiempos donde se habla de la tecnología, información, sociedad del conocimiento, etc., aprovecho la oportunidad de describir lo poderosa que es la hoja de cálculo de excel, pero voy a referirme en particular a una de las herramientas la cual se denomina Solver, y se puede ubicar en el menú principal en la opción Herramientas, al pulsar este icono aparecerán varias opciones y ahí encontraran dicha instrucción, ella resuelve problemas lineales y enteros utilizando el método más simple con límites en las variables y el método de ramificación y límite, implantado por John Watson y Dan Fylstra de Frontline Systems, Inc. Es de hacer notar que estos problemas se presentan en las ciencias administrativas y es requisito indispensable en casi todas las áreas de ciencias sociales, ingeniería, y en cualquiera de las carreras universitarias como Ciencias Estadísticas, Economía, Administración, entre otras, allí se estudia en una cátedra llamada Investigación de Operaciones, en ella se construyen modelos para el análisis y la toma de decisiones administrativas, los cuales en tiempos remotos se utilizaban algoritmos muy complejos entre ellos el del método simplex y el dual, estas técnicas manualmente son complejas, pero con la tecnología aparecieron softwares para resolver sendos problemas entre ellos se encuentra el más conocido que es el "LINDO", pero hoy tenemos la oportunidad de resolverlos muy fácilmente mediante la hoja de cálculo de excel y el paquete agregado llamado "SOLVER" que optimiza los modelos sujetos a restricciones, como los modelos de programación lineal y no lineales, la cual permite obtener las soluciones óptimas para un modelo determinado, y dependiendo de los niveles de la organización se tomen las mejores decisiones para resolver los conflictos de una empresa.

Proceso de construcción de modelos
1- Definir variables de decisión
2- Definir la función de objetivos
3- Definir las restricciones

Utilidad o perdida = PX - CX - F
MAX Z = PX - CX - F
S.A

Donde:
P= Precio
C= Costo
X= Utilidades vendidas
F= Costo fijo

X<= U
X<= D
X<= O

2. Ejemplo de cómo usar "SOLVER"

Andrés Z. Es presidente de una microempresa de inversiones que se dedica a administrar las carteras de acciones de varios clientes. Un nuevo cliente ha solicitado que la compañía se haga cargo de administrar para él una cartera de 100.000$. A ese cliente le agradaría restringir la cartera a una mezcla de tres tipos de acciones únicamente, como podemos apreciar en la siguiente tabla. Formule usted un modelo de Programación Lineal para mostrar cuántas acciones de cada tipo tendría que comprar Andrés con el fin de maximizar el rendimiento anual total estimado de esa cartera.

Acciones	Precio ($)	Rendimiento Anual Estimado por Acción ($)	Inversión Posible ($)
Navesa	60	7	60.000
Telectricidad	25	3	25.000
Rampa	20	3	30.000

Para solucionar este problema debemos seguir los pasos para la construcción de modelos de programación lineal (PL):
1.- Definir la variable de decisión.
2.- Definir la función objetivo.
3.- Definir las restricciones.

Luego construimos el modelo:
MAX Z = 7X1 + 3X2 + 3X3
S.A.:
60X1 +25X2 + 20X3 <= 100.000
60X1 <= 60.000
25X2 <= 25.000
20X3 <= 30.000
Xi >= 0

A continuación se construye el modelo en una hoja de cálculo de excel de la siguiente manera:

En la fila 2 se coloca la variable de decisión la cual es el número de acciones y sus valores desde la B2 hasta la D2.
En la fila 3 el rendimiento anual y sus valores desde B3 hasta D3.
En la celda E3 colocaremos una formula la cual nos va indicar el rendimiento anual total, =sumaproducto($B$2:$D$2;B3:D3).
Desde la fila B5 hasta la D8 colocaremos los coeficientes que acompañan a las variables de decisión que componen las restricciones.
Desde la E5 hasta la E8 se encuentra la función de restricción (LI) y no es mas que utilizar la siguiente formula =sumaproducto($B$2:$D$2;B5:D5) la cual se alojaría en la celda E5, luego daríamos un copy hasta la E8.
Desde la F5 hasta F8 se encuentran los valores de las restricciones.
Desde la G5 hasta G8 se encuentra la holgura o excedente.
Una vez completada la hoja de cálculo con el modelo respectivo ¡GRABE SU HOJA!, y seleccione "Solver…" en el menú de "Herramientas", ahí tendrá que especificar dentro del cuadro de dialogo de Solver:

• La celda que va a optimizar
• Las celdas cambiantes
• Las restricciones

Así tendremos la siguiente pantalla:

Como se puede observar en la celda objetivo se coloca la celda que se quiere optimizar, en las celdas cambiantes las variables de decisión y por último se debe de complementar con las restricciones. Una vez realizado estos pasos deben pulsar el icono de "Opciones" y debe hacer clic en "Asumir modelo lineal" y enseguida el botón de "Aceptar". Luego haga clic en el botón de "Resolver" para realizar la optimización, lea detenidamente el mensaje de terminación de Solver y ahí observará si se encontró una solución o hay que modificar el modelo, en caso de haber encontrado una solución óptima usted podrá aceptar o no dicha solución, luego tendrá oportunidad de analizar un informe de análisis de sensibilidad para luego tomar la mejor decisión.

En nuestro ejemplo el máximo rendimiento anual fue de 12750$, y la cantidad de acciones a comprar serían 750, 1000 y 1500 para Navesa, Telectricidad y Rampa respectivamente. De está forma podemos observar la potencia que tiene el solver, para
mayor información sobre el tema, en la ayuda de la hoja de cálculo de excel o en libro de Investigación de Operaciones en la Ciencias Administrativas, autor: Eppen quinta edición, Editorial Prentice Hall tendrán una mayor explicación.